Lógica:
A lógica é um raciocínio criado por Aristóteles que serviu como base para criação da álgebra matemática. Neste texto será dito como a lógica é usada e a definição dela.
Aristóteles foi de extrema importância para a introdução científica no mundo. A lógica dele é baseada na Lei da não contra indicação, Lei do terceiro excluído.
Lei da não contra indicação: Ela diz que uma proposição verdadeira não pode ser falsa e uma proposição falsa não pode ser verdadeira. Nenhuma proposição, portanto, pode ser os dois ao mesmo tempo. A lei da não-contradição é representada do seguinte modo:
Exemplo: Não ("a bola é redonda" e "a bola não é redonda")
Uma proposição não pode ser verdadeira e falsa, para obedecer ao principio da não contradição.
A lei do terceiro excluído: (em latim resumida na expressão tertium non datur), é um princípio cujo enunciado consiste no seguinte: "ou A é x ou é y e não há terceira possibilidade". É representada da seguinte maneira:
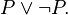
Exemplo: Ou este homem é Sócrates ou não é Sócrates.
Uma proposição só pode ser verdadeira se não for falsa e só pode ser falsa se não for verdadeira, porque o terceiro valor é excluído.
Isso funciona como base para Teoria do Silogismo:
Todo homem é mortal.
Sócrates é homem.
Sócrates é mortal.
A lógica usada pela computação foi inventada por George Boole. Conhecida como Álgebra Booleana.
A Álgebra Booleana tem como finalidade lidar com técnicas proposicional, isto é trabalhar somente com setência verdadeira e falsa. Os Símbolos usados são:
0: Falso
1: Verdadeiro
¬: Não
^: E
V: OU
=: Equivale
Ex: a v a = a
A Álgebra Booleana não foi imediatamente usada na época, ela só foi utilizada aproximadamente 100 anos depois da sua criação.
Gottlob Frege notou que os matemáticos da época frequentemente cometiam erros em suas demostrações, para corrigir isto ele criou a Lógica de Predicados.
A Lógica de Predicado é baseada no Lógica de Proposição. Nela foi acresentado a quantificação.
: para todo x, ¢ é verdadeiro.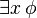
: para algum x, ¢ é verdadeiro.^: E
v: OU
->: Implica
<->: Se, somente se
=: equivale
Ex: a -> b = ¬a v b
Um cálculo de predicados consiste em:
- Regras de formação(definição recursivas, função que se refere a si própria, para dar origem de fórmulas bem-formadas);
- Regra de Transformação (Regras de interferência para derivar teoremas);
- axiomas (Uma sentença ou proposição que não é provada ).
Fonte: Wikipédia.
